Study of barkhan dune movement

The accelerated expansion of deserts due to global warming increasingly threatens inhabited areas, as can be seen in cities like Nouakchott in Mauritania. The movement of sand dunes is a key factor in this phenomenon, causing the destruction of infrastructure and submerging roads.

Studying dunes in nature is challenging due to their large size and very slow movement. As a result, researchers have turned to methods such as small-scale modeling and numerical simulations to better understand the phenomena governing their behavior—and subsequently to combat the threat of sand encroachment.

We sought to implement our own version of these methods, drawing inspiration in particular from the doctoral research of Pascal Hersen at ENS laboratories. Our goal was to assess how well these methods reflect reality and how they help us understand the physics of dunes.

The barkhan dune

The barkhan dune is a crescent shaped dune typical of deserts like the Sahara, where the wind is unidirectional on average. This gives the dune a very symetrical crescent-like shape. The wind blows up the windward face, and arrives at the top, to the slip face, which is much steeper and is flanked by two horns. The turbulent flow behind the dune creates a recirculation bubble, leading to this characteristic shape. This phenomenon is caused by the detachment of the boundary layer, as the aspect ratio becomes too large, preventing the streamlines from “hugging” the terrain.

For barchan dunes, we can define their length \(l\) (from the front to the tip of the horns) and their width \(W\)(between the two horns) and their height \(h\). Experimental observations show that the dimensions of a barchan dune are proportional to each other, with the ratios \(l/W = 1\) and \(h/W = 0.1\).

Dynamics

To effectively combat sand encroachment, we must closely examine the movement of barchan dunes and understand their dynamics. The movement of the dune is driven by wind acceleration, which picks up sand on the windward face and deposits it on the slip face.

We take a ‘slice’ of dune of length \(L\) perpendicular to the \(Ox\) axis which we can suppose follows the direction of the wind on the surface plane and define the the mass flux of sand per unit width \(Q(x,t)\) at position \(x\) and time \(t\). Assuming the barkhane dune doesn’t deform, we can use conservation of mass :

Mass balance gives us

With \(m = \rho h(x,t)Ldx\) we get

The non deformation of the dune gives \(h(x, t+dt) = h(x -ct, t)\) and then

By replacing (2) in (1) we get \(\frac{\partial h}{\partial x} - \frac{1}{\rho c} \frac{\partial h}{\partial x} = 0\)

Integrating over \(x\) between \(x = 0\) and the top of the dune \(x = x_{s}\) and isolating \(c\), we define \(q_{s} = \frac{Q(x_{s}, t)}{h_{s}}\) the surface flux of sand at the dune crest (in \({m}^2\text{.s}^{-1}\)) and \(q_{0}\) at the base:

Knowing the proportionnality between the length, width and height, we can also write more generally :

Minimal dune length

Experimental observations reveal that no barchan dune is smaller than 1 meter. This minimum size highlights the existence of a characteristic length governing dune physics. As wind passes over the dune, it picks up sand, but there is a delay between the actual sand flux and the saturated sand flux (“as the wind picks up sand, it slows down, grains fall, and equilibrium is achieved”).

This allows us to define \(l_{sat}\), the saturation length of the flux. Experimental observations also show that \(l_{sat}\) corresponds to the minimum size of a dune. Using an order-of-magnitude analysis, \(l_{sat}\) is proportional to \(l_{drag}\), where:

Approximately, \(l_{sat} ≈ 10 × l_{drag}\) , giving \(l_{sat} ≈ 7.5 m\).

Experimental setup

The existence of a characteristic length allows us to assert that it is possible to study barchan dunes on a small scale. This characteristic length enables us to bridge the gap between different scales. By scaling down our centimeter-sized dunes using \(l_{drag}\), we can compare them to real dunes. To create dunes in the laboratory, we need to follow two principles:

1) Reduce \(l_{drag}\): To minimize the smallest size of the dunes, we placed the experiment in a denser medium : water. 2) Simulate a unidirectional flow: Similar to those found in deserts.

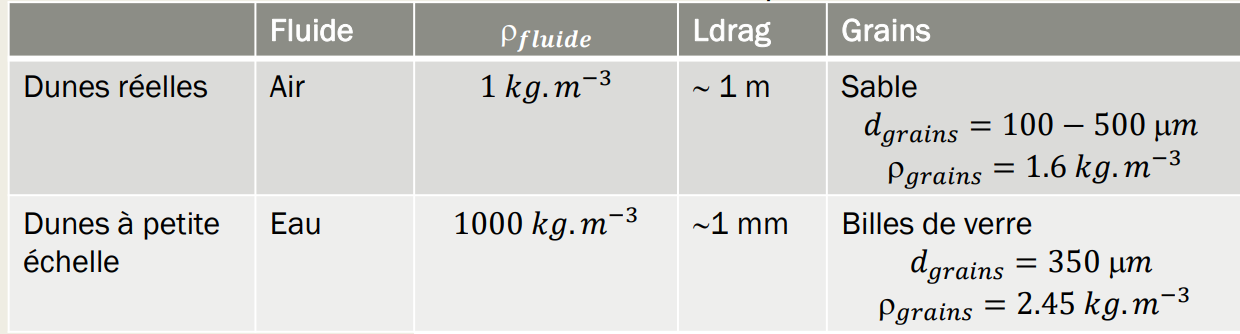
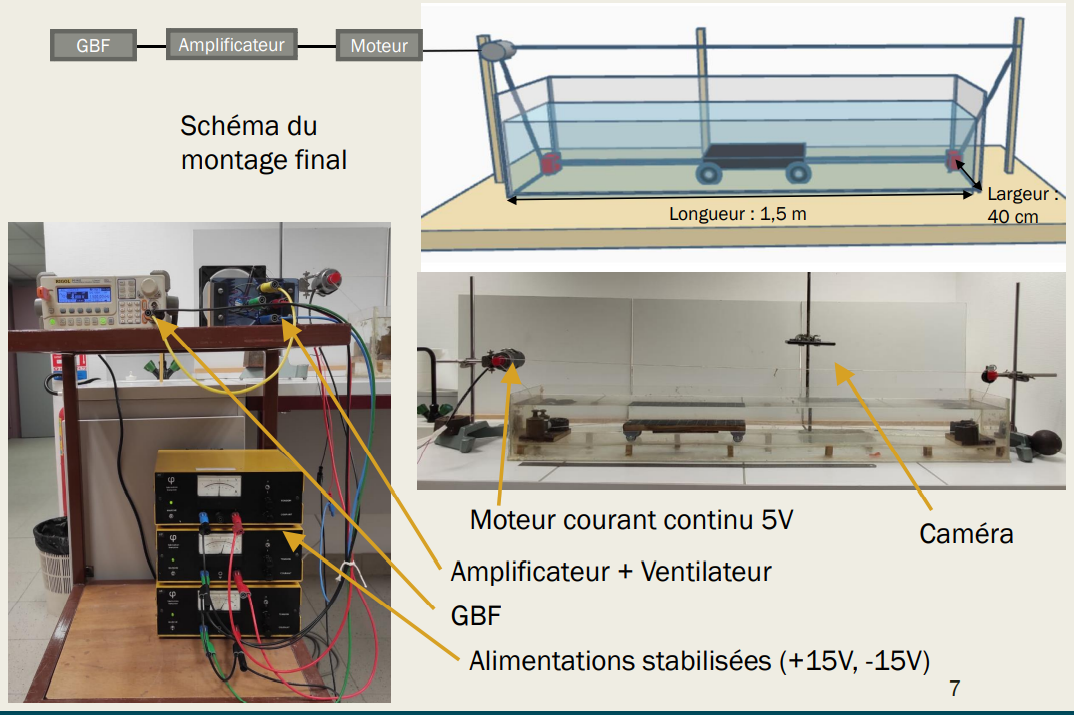
We developed the following setup: To simulate unidirectional flow, we implemented a system with a moving plate onto which we placed a pile of glass beads with known density and diameter. The use of glass beads allowed us to maintain precise diameters and work consistently with the same parameters. We opted for an initial conical pile, which was easy to reproduce identically, ensuring consistent initial conditions. Our goal was to move the plate asymmetrically: a fast forward movement and a very slow return, simulating unidirectional wind (37 cm/s forward, 6 cm/s backward, covering approximately 80 cm forward and 80 cm back to return to the initial position).

The experiment was monitored by taking photos after each forward and backward movement of the plate. The plate was marked with a grid to measure dune displacement. Using tracking software, we measured the characteristic dimensions and displacement of the dunes. An attempt to measure dune height using a laser was unsuccessful.

We observed that, after a brief transient regime with significant erosion of the initial conical pile, the barchan shape emerged, and the dune entered a steady state where it lost much less material.

You can also put regular text between your rows of images. Say you wanted to write a little bit about your project before you posted the rest of the images. You describe how you toiled, sweated, bled for your project, and then… you reveal its glory in the next row of images.

Simulation

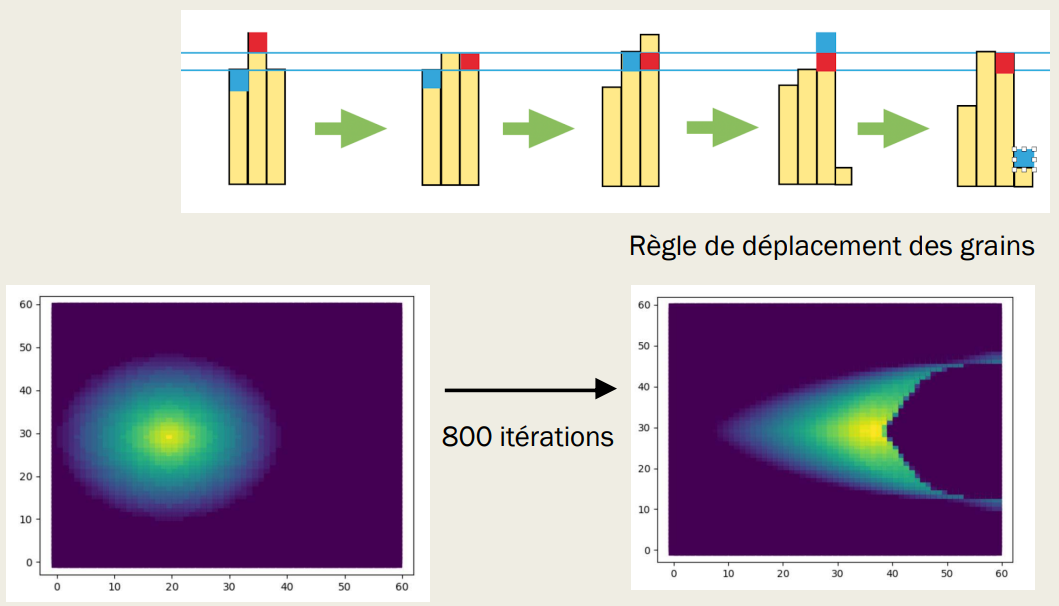
Computational modeling is also a very relevant option for studying dune movement and predicting their displacement in the desert. We aimed to create a Python program, based on simple rules, that would allow us to study these dune movements. Our modeling is done using a number array/matrix system. Each cell in the matrix is associated with a number that represents the height of the sand pile at that cell.

A first function, cone_pile, allows us to create an initial pile, similar to the one we built in our experimental setup.

We then developed a simple rule to simulate the movement of sand grains due to the wind flow over the pile:

1) A function, unidirectional_rule, moves a sand grain from one pile to the pile behind it, based on the wind direction, under two conditions:
- The pile in front must be strictly smaller than the pile being studied.
- The pile behind can be at most the size of the current pile + 1.

2) A function, collapse, simulates the collapse of grains on the avalanche face by measuring the height difference between one column and the next. If the difference is positive, a random number of grains falls onto the following column.

Results

The longevity of the barkhanoid shapes obtained in the small-scale experiment, as well as the dunes simulated in Python, encourages us to make a link between these models and real dunes to study whether these models are consistent with measurements taken in nature. First, we observe that the simulated dunes and the small-scale dunes both present a crescent shape with two horns at the ends.

Constant ratios

To verify whether these models allow us to form real barkhanes, we need to study the dimensions of the dunes obtained. The characteristic length \(l_{drag}\) introduced at the beginning would allow us to link small-scale dunes with real dunes. For the computer simulation, an arbitrary unit of one meter per element was used. The experimental data is compared with real barkhane dunes observed by a researcher and with the experiment of the scientist Pascal Hersen, who conducted a similar experiment to ours, for which we did not include uncertainties as no information was provided.

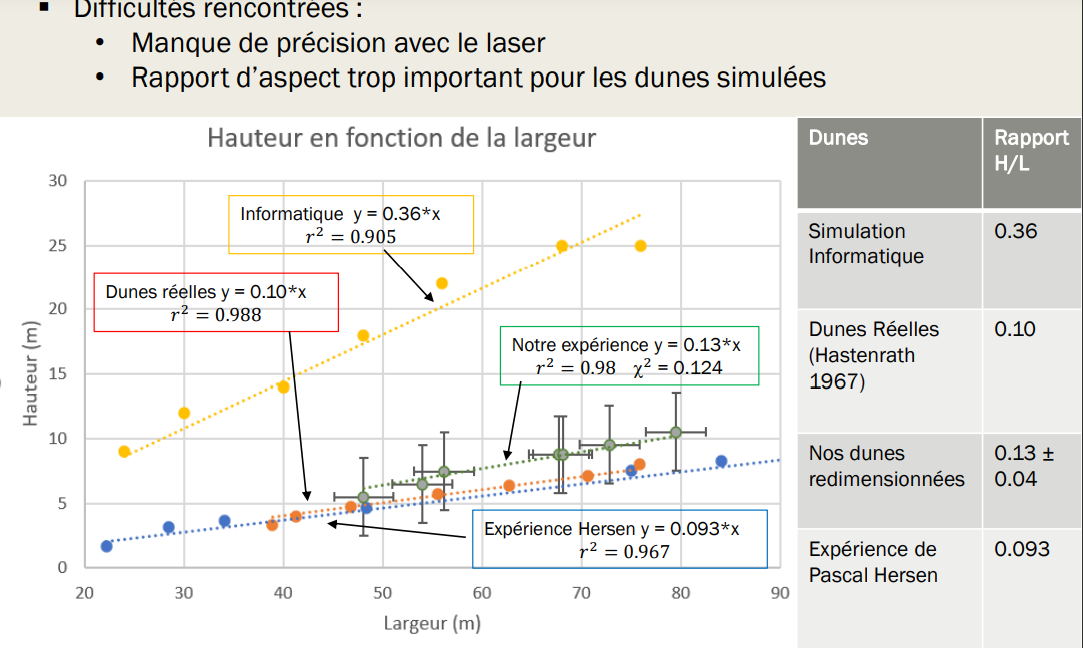
Length as a Function of Width After resizing the measurements by \(l_{drag}\), we observe that the small-scale dunes overlap with real dunes and follow the same experimental laws: width and length are indeed equivalent. Therefore, we can conclude that the experiment is successful. The computer simulation also verifies the experimental criteria observed for the barkhanes.

Height as a Function of Width However, we encountered problems with measuring height. For small-scale barkhanes, although the general magnitude of the dimensions is correct, measuring the height (less than 1 cm) proved difficult. We attempted to measure it with a laser, but the precision was very poor. The dunes often had very similar heights, making them impossible to distinguish. For the simulated dunes, a proportionality of 0.4 is found, which does not correspond to the experimental observations.

This is partly due to the discrete nature of the modeling, which shows its limits. For aspect ratios that are too low, the rules do not work well and tend to exaggerate the heights. The formation of larger dunes, reducing the discrete nature, seems to allow the formation of dunes that are more faithful to reality.

Displacement

To truly validate the models, we must ensure that the small-scale dunes and simulated dunes follow the same speed law as real dunes. This is even the most important quantity for sand dune prevention.

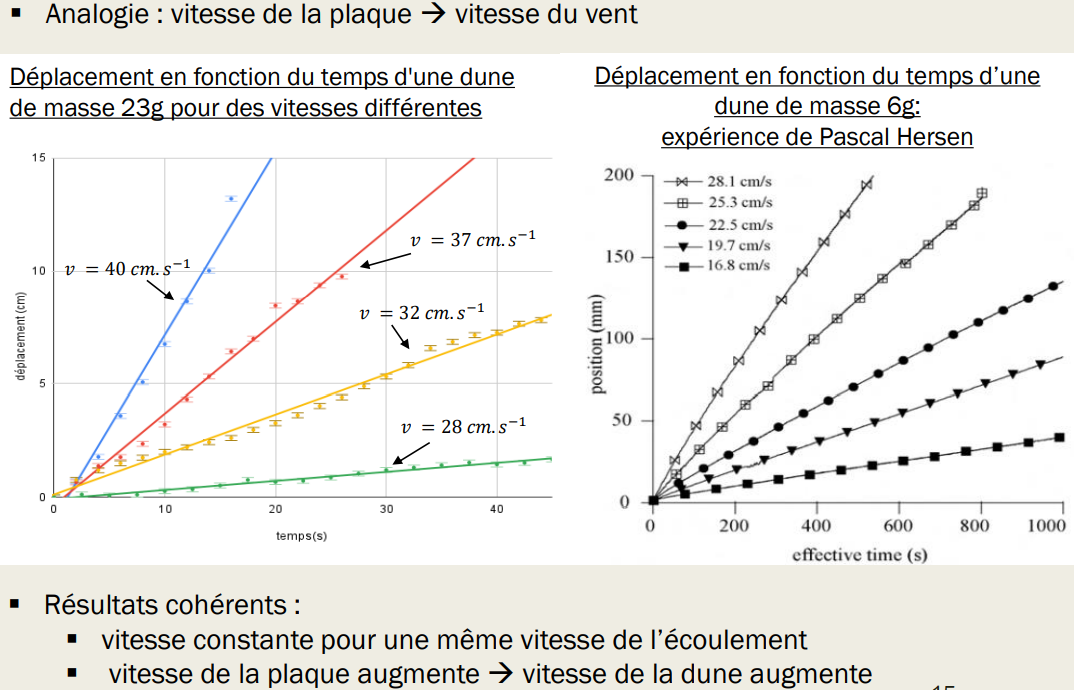
Displacement as a Function of Plate Speed We first sought to study the influence of the plate speed, which can be assimilated to the apparent wind speed in the desert, on the displacement of the dune. We observe that for a given plate speed, the dune speed is constant, highlighting the stability of the barkhane shapes. They lose little sand over time and change shape minimally. Additionally, we qualitatively observe that increasing the plate speed increases the dune speed, with a limiting speed above which it becomes unstable. This result was also obtained by the scientist Pascal Hersen.

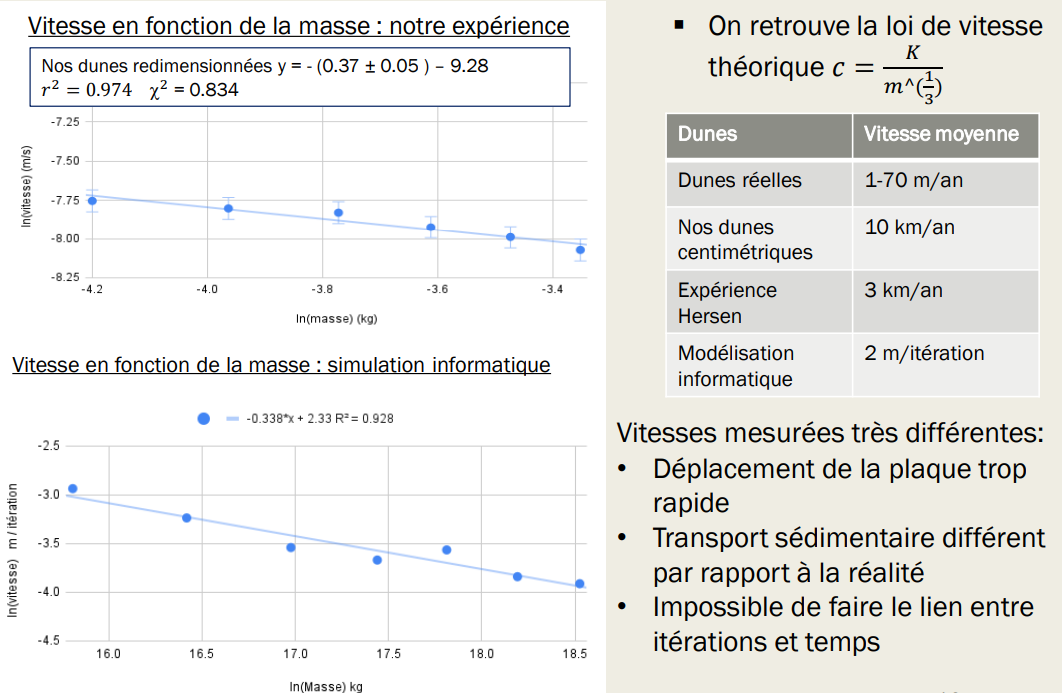
Displacement as a Function of Mass In addition to these qualitative results, we wanted to more precisely verify whether our small-scale dunes and simulated dunes follow the theoretical speed law presented earlier. A mass balance on the dune allows us to relate mass and height. However, measuring height is difficult, so we use the constant ratios to link speed and mass. We approximate by neglecting the losses at the horns because the dune’s displacement speed is high compared to the characteristic times of its morphological evolution due to losses. We study the dune’s displacement on the plate as a function of time to obtain its speed. In both situations, we observe that there is indeed a link between the dune speed and the cube root of its mass. However, we observe large differences in the constant q of proportionality, which depends on the flux at the crest.

Thus, as found by Pascal Hersen, our dunes are too fast: this may be due to the plate speed being too high. Indeed, with slower movements, Pascal Hersen has already managed to reduce the speed of the dunes, and it is difficult to link the flow speed in our experiment with the plate speed. For the computer simulation, we quickly reach the limits of the model. First, it is difficult to link the number of iterations in the program with real time. Additionally, the arbitrary decision to set a value of 1 = 1 meter for the analogy once again shows the limits of this approach: more coherent comparisons would likely require forming much larger dunes, as seen with the height.