Cooperative Inverse Reinforcement Learning
Ecole Polytechnique Collaborative and Reliable Learning Course
In reinforcement learning (RL), an agent interacts with its environment, maximizing its cumulative reward over time and therefore learning a policy dictating its actions based on states and observations. However, one critical issue in RL is the alignment problem: if the reward function is not correct, the result computed will not be correct either. The Inverse Reinforcement Learning (IRL) framework tries to address this by estimating reward functions by observing behaviors that maximize that reward function (for instance, a recommendation algorithm that infers your tastes from the videos you watch). The Cooperative Inverse Reinforcement Learning (CIRL) framework goes one step further: it introduces an agent which has perfect knowledge of the reward function (referred to as the ”human” in the article), which is incentivized to convey it to another agent with its behavior (the other agent is called a ”robot”). Although this work was initially developed for robotics, the terms ”human” and ”robot” can refer to a much broader class of agents.
This project in collaboration with Martin Drieux and Edouard Rabasse for Ecole Polytechnique’s Collaborative and Reliable Learning course, is a study of Cooperative Inverse Reinforcement Learning (CIRL) based on the article by the same name of Hadfield-Menell et al. (Neurips 2016). We propose an implementation of the paper and propose a more general framework.
Apprenticeship CIRL and Implementation
In their work, the authors introduce Apprenticeship CIRL, a turn-based game composed of 2 phases : a learning phase during which only the human takes actions, and a deployment phase where only the robot acts. It can be shown that this framework is in fact a CIRL, and, knowing the robot greedily maximizes the from the mean \(\theta\) from its belief in the deployment phase:
\[\pi_{R}^* = \arg\max_{\pi^R} \mathbb{E} \left[ R(s, \pi_{R}(s) \mid \theta) \right]\]The key insight here is that, knowing this robot behaviour, the human’s best response may not a demonstration by expert (DBE) maximizing its own reward.
To establish some results on ACIRL and possible best responses, the paper uses a specific framework and makes some assumptions without stating them explicitly. Here are these assumptions:
-
Rewards are a linear combination of state features for a certain feature function:
\[\phi : R(s, a^\mathcal{H}, a^\mathcal{R}; \theta) = \phi(s)^\top \theta\]In that case, two policies with the same expected feature counts $\mu$ will have the same values.
\[\begin{align} V^\pi &= \mathbb{E} \left[ \sum_{t=0}^\infty \gamma^t R(s_t \mid \pi) \right] \\ &= \theta \cdot \mathbb{E} \left[ \sum_{t=0}^\infty \gamma^t \phi(s_t) \mid \pi \right] \\ &= \theta \cdot \mu(\pi) \end{align}\]This means that a learned policy that matches the feature counts of the observed policy will be as good as the demonstration for any given \(\theta\).
-
R uses an IRL algorithm that computes its belief on \(\theta\) specifically by maximizing feature counts, as Maximum-Entropy IRL for example.
These two assumptions ensure that the robot’s policy
\[\pi_R^* = \arg\max E_{\pi}[\Phi(\pi)] \cdot \theta\]will match the expected feature counts of the learning phase. In fact, we see through this equation that there is no reason the expected feature counts match if the belief through IRL wasn’t computed through an algorithm that does. This underlying assumption wasn’t detailed in the paper. In fact, there exist IRL algorithms such as Adversarial IRL that do not compute a belief on \(\theta\) by matching expected feature counts.
Knowing this feature count matching, the paper proposes the following heuristic for the human, to generate better demonstrations by matching the feature counts with those of the distribution of trajectories induced by \(\theta\) : \(\phi_{\theta}\)
\[\tau^H \leftarrow \arg\max_{\tau} \underbrace{\phi(\tau) \cdot \theta}_{\substack{\text{Sum of rewards}\\\text{for the human}}} - \underbrace{\eta\|\phi_\theta - \phi(\tau)\|^2}_{\substack{\text{Feature}\\\text{dissimilarity}}}\]We propose an implementation of this feature-matching approach (see code and paper).
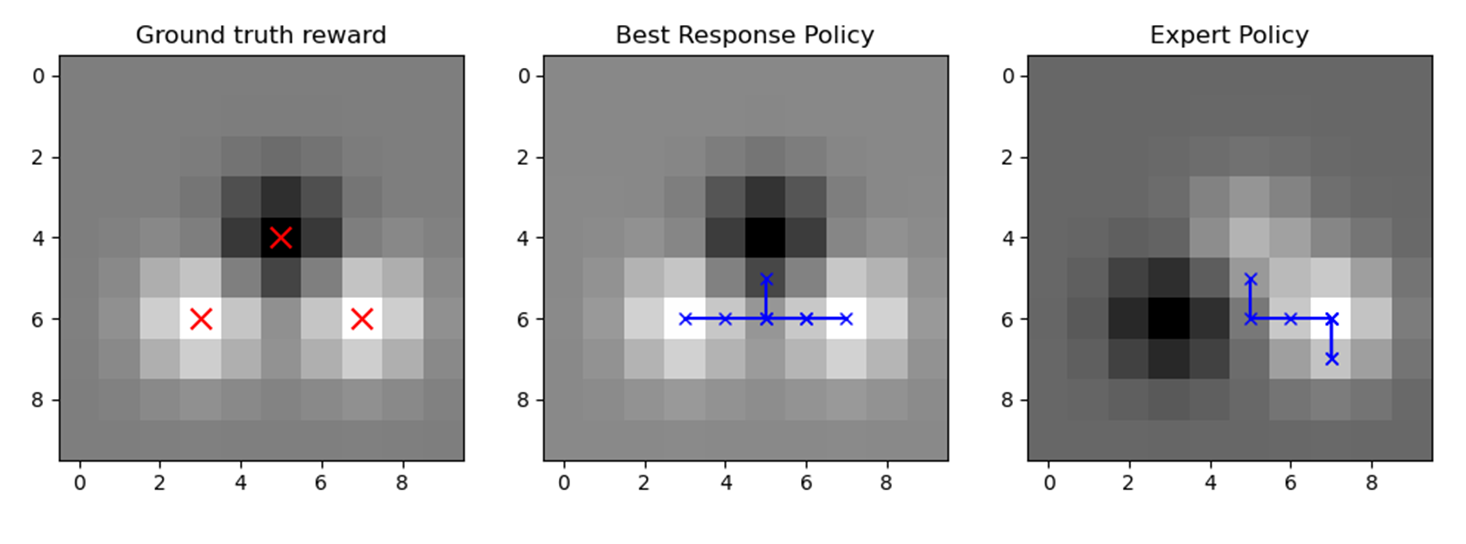
Figure 1 illustrates the impact of the feature count matching term in the best response in this example with three features. The best response trajectory explicitly goes to the two lower feature centers instead of just maximizing its own reward (DBE). The inferred \(\theta\) by the robot and therefore the reward structure are closer to the ground truth in the best response thanks to the better demonstration.
We compare the results of the best response and expert trajectories on three similarity measures:
-
Regret: the difference in the value of the policy that maximizes the inferred \(\hat\theta\) and the value of the policy that maximizes the true \(\theta\).
\[regret = V^{\pi_{\hat\theta}} - V^{\pi_{\theta}}\] -
The KL divergence between the trajectory distributions induced by \(\theta\) and \(\hat\theta\).
\[D_{KL}(P_{\hat\theta} \| P_{\theta}) = \sum_{s \in \mathcal{S}} \sum_{a \in \mathcal{A}} P_{\hat\theta}(s,a)\log\frac{P_{\hat\theta}(s,a)}{P_{\theta}(s,a)}\] -
The L2 Norm as a simpler proxy for the regret:
\[\|\theta - \hat{\theta}\|_2\]
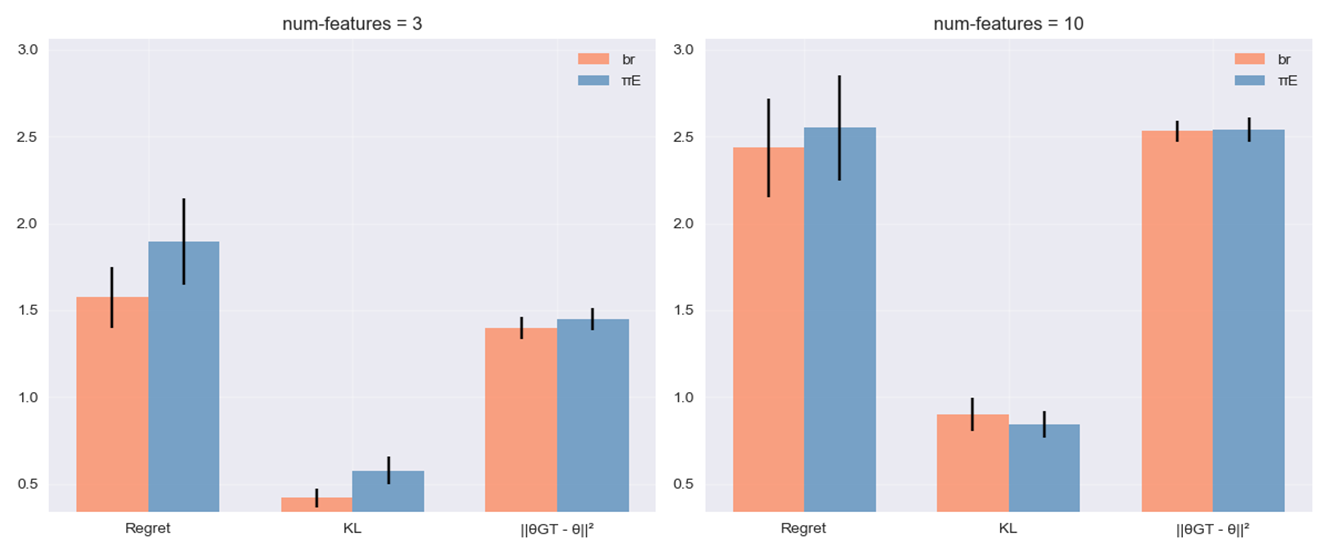
The results are less conclusive than the ones presented by the paper, as the standard deviation from the mean is large, especially for the regret. Nevertheless, the best response generally makes the robot infer better results, closer to the true \(\theta\), than the expert demonstration.
True CIRL
After introducing the CIRL framework, the paper makes a number of strong assumptions in order to apply it to its robotics application. This approach results in a loss of generality which does not fully tap into the whole potential of the framework introduced. Indeed, the case developed in the above part has more to do with optimal teaching than a collaborative game (which is still interesting but more restrictive). We therefore wanted to work in a more general setting and use an algorithm specifically devised for the structure of CIRL problems, and which can solve them without loss of generality. This approach has enabled us to avoid using approximation tricks with functions developed for other applications (as above with the specific Maximum-Entropy IRL algorithm).
In this part, we develop an algorithm to compute exact solutions of the CIRL, that is more efficient than default methods. There exist several standard algorithms to fully solve POMDPs. One of the exact methods is the Witness Algorithm, which constructs optimal conditional plans for the POMDP by iteratively refining the set of candidate plans. The tremendous cost of computation comes from the fact that the action space considered is extremely large : for each action, we have to consider every combination of a robot action and of every possible response plan of the human to a given \(\theta\). However, it is possible to reduce the complexity by this term.
Indeed, in one of the proofs in the original article, the authors highlight that the human knows the policy of the robot, and can anticipate its response to any action. That is what we are going to exploit here: instead of considering every possible human action we will only take the optimal one to maximize future reward (this can be computed thanks to the recursive nature of the algorithm). This approach was inspired by an article on a similar subject.
This enables us to adapt the Witness Algorithm through a double recursive structure, which converges as the lengths of the conditional plans decrease at each call.
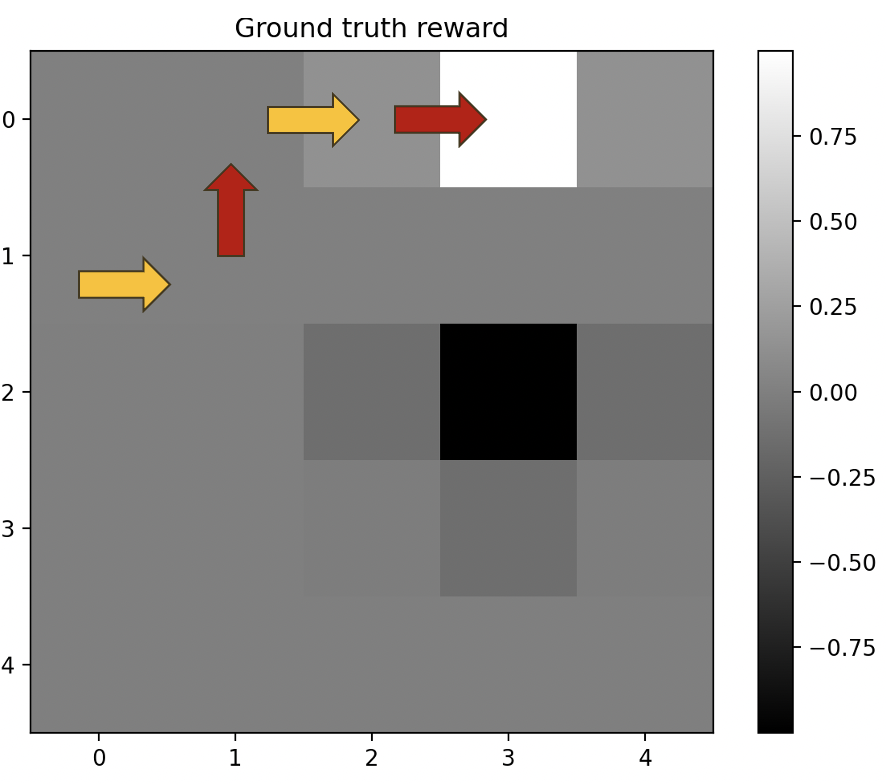
We coded from scratch a general solver, which outputs optimal policies if a valid CIRL problem is given as an input, as well as an initial belief state. To apply this new approach, we chose to work on a step by step collaborative version of the problem developed in the article. The “robot” and the “human” are 2 players which can control a moving object. They both choose a decision at each turn, and the robot updates its belief based on the human’s actions. Here, the feature centers (which correspond to gaussians) can have either, positive, negative or zero value (\(\theta_i \in { -1, 0, 1 }\)). In figure 4, we see that the human indicates that the high value spot is up, and the robot acts coherently as this single action is sufficient for it to understand that the higher spot has a positive value (its belief is updated in this way).
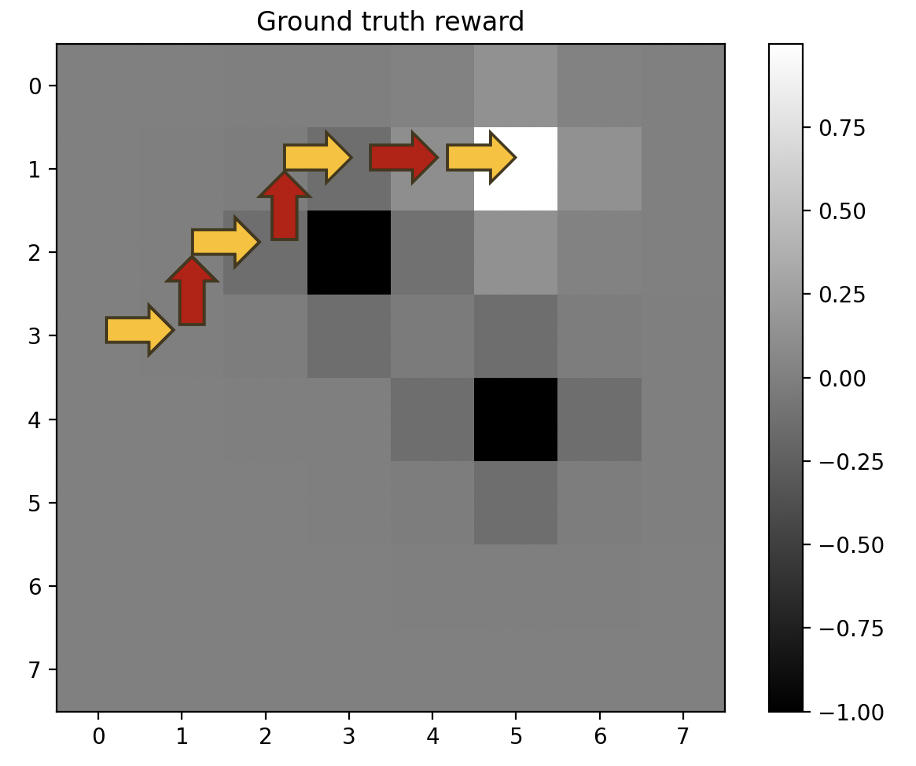
The example in figure 5 illustrates that the robot does not have perfect information : on its second step, it chooses to go right (which is suboptimal) because the human has not yet made any action that indicates that the spot in (3,2) has a negative value (the human would have gone up if it did). The robot “understands” this (which means it updates its belief accordingly) afterwards, as the moves towards the spot in (5,1) indicate.
This example, and its subtleties illustrate the class of complex problems that can be solved with the CIRL approach.
Conclusion
The Cooperative Inverse Reinforcement Learning (CIRL) framework, introduced in the foundational paper, offers an innovative approach to solving the alignment problem in human-robot collaboration. By reformulating CIRL as a Partially Observable Markov Decision Process (POMDP), the original work establishes a solid theoretical foundation and demonstrates its potential in controlled environments.
We implemented a turn-based Apprenticeship CIRL (ACIRL) framework in a 10x10 gridworld environment, addressing gaps in the original methodology with detailed explanations of key processes, such as trajectory generation, feature matching, and maximum entropy IRL. Additionally, we implemented a general CIRL algorithm, which is more precise and comprehensive than ACIRL.
A major limitation of the original framework is its computational complexity. To address this, we drew inspiration from recent research. By automating the human’s optimal actions and leveraging recursive updates, we reduced the action space size and computational cost, making policy computation more efficient—though it remains computationally expensive.
Our work focused on fully leveraging the formalism introduced in the article. Future directions could include exploring scenarios where the “human” has only partial information or where multiple robots are involved